
Wie sieht der 3-dimensionale Schatten
eines 4-dimensionalen Würfels aus?
Wenn man diese Frage liest, gerät die eigene Vorstellungskraft ins Wanken. Zu recht, denn 4-dimensionale Würfel gibt es (in der Realität) nicht und sie überfordern unsere Vorstellungskraft, da die auf 3 Dimensionen trainiert ist. Nichts desto trotz erlauben uns Mathematik und Logik Wissen ausserhalb unserer Vorstellungskraft zu erlangen. Das Beispiel hier ist ein einfaches aber exemplarisches.
Zuerst nehmen wir die Begriffe der Aufgabe auseinander. Im wesentlichen sind es drei: Dimension, Schatten und Würfel.

Wir leben in einer 3-dimensionalen Welt. Alles was wir anfassen können ist 3-dimensional. Bei vielen Dingen sind wir aber nicht an allen drei Dimensionen gleichermassen interessiert. Bei einem Blatt beispielsweise sind Höhe und Breite meist von grösserer Bedeutung als die Dicke. Deshalb behandeln wir das Blatt meistens als wäre es 2-dimensional. Fäden wiederum sehen wir 1-dimensional.
Bei der Dimension muss man auch zwischen dem Objekt und dem Raum, in dem es sich befindet unterscheiden. Ein Strich auf einem Blatt ist beispielsweise ein 1-dimensionales Objekt in einem 2-dimensionalen Raum. Ein Objekt kann maximal die gleiche Dimension haben wie der Raum, in dem es sich befindet.

Was wir im Alltag als Schatten oder Schattenwurf bezeichnen wird in der Mathematik als Projektion bezeichnet. Ein Schattenwurf in der Realität bildet die Umrisse eines 3-dimensionalen Objekts auf eine 2-dimensionale Fläche ab. Es reduziert in dem Sinne die Anzahl Dimensionen um eins. Der Schatten selbst ist kein reales Objekt, da unsere Realität auf drei Dimensionen basiert, sondern nur eine Abfolge von Hell und Dunkel.
Der in der Aufgabenstellung geforderte Schatten hat die gleiche Aufgabe: Er reduziert die Anzahl Dimensionen um eins, dieses mal einfach von vier auf drei statt von drei auf zwei. Das Ergebnis wird also eine messbare Länge, Breite und Höhe haben. Und vor allem, da er 3-dimensional ist: man kann den Schatten als Modell herstellen und dieses auch anfassen!
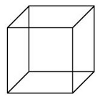
Was ein Würfel ist, sollte weitgehend klar sein. Wir werden hier aber immer den Fokus auf die Kanten des Würfels legen. Dies vor allem damit wir alle Kanten erkennen können. Das rechts ist übrigens kein Würfel, sondern die 2-dimensionale Projektion eines Kantenmodells eines (3-dimensionalen) Würfels. Denn Bildschirme arbeiten 2-dimensional. Unser Gehirn erkennt aber, dass der Ursprung dieses Bildes ein 3-dimensionaler Würfel war, und lässt diesen in unserer Vorstellungskraft auferstehen. Das gilt nach wie vor auch für 3D-Bildschirme. Auch deren Bild ist flach. Sie unterstützen unsere Vorstellungskraft aber noch besser, indem sie pro Auge ein leicht anderes Bild präsentieren.
Von einem Faden wollen wir die Länge wissen, von einem Blatt Länge und Breite, von einem Holzquader Länge, Breite und Höhe. Als Mathematiker fragt man sich nun, was kommt als nächstes. Ok, mehr als 3 Dimensionen kennt unsere Realität nicht. Aber die Mathematik hat von ihren Regeln her keine solche Grenzen. Die Mechanismen der Mathematik kann man problemlos erweitern.
Damit wir beim Durchbrechen der dritten Dimension unsere Vorstellungskraft nicht komplett überfordern, nehmen wir zwei einfache Objekte – Würfel und Tetraeder (Dreieckspyramide) – und gehen zuerst in die andere Richtung.
Die 2-dimensionalen Gegenstücke zu den beiden Körper sind das gleichseitige Dreieck und das Quadrat. Damit wir auch bei den Begriffen die Systematik möglichst klar erfassen, werden wir ab jetzt teilweise auch von 2- und 3-dimensionalen Würfeln reden, wenn wir Quadrat und Würfel meinen, und von 2- und 3-dimensionalen Dreiecken, bei gleichseitigem Dreieck und Tetraeder.
Als zweites werden wir den Weg vom 2- zum 3-dimensionalen Würfel respektive Dreieck und wieder zurück mal anders beschreiben.
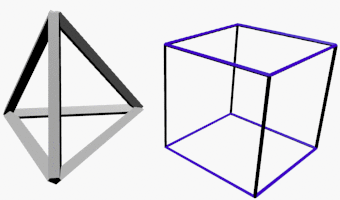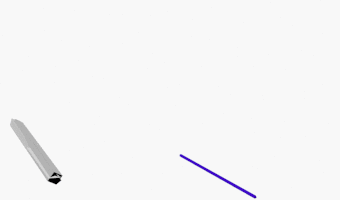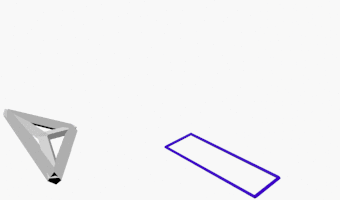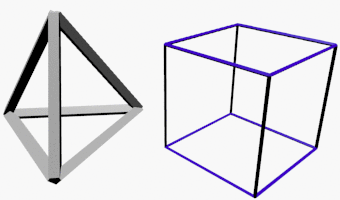
Man kann diese Transformation noch weiter ziehen bis hin zu 0 Dimensionen. Es sind die genau gleichen Vorgänge. Bei beiden entsteht zuerst eine Strecke, die somit sowohl ein 1-dimensionaler Würfel als auch ein 1-dimensionales Dreieck ist, dann ein Punkt, der somit sowohl ein 0-dimensionaler Würfel als auch ein 0-dimensionales Dreieck ist. Das klingt etwas komisch, ist aber konsequent und durchaus logisch.
Betrachten wir nun von was die verschiedenen n-dimensionalen Würfel und Dreiecke begrenzt werden. Klar ist, dass ein n-dimensionales Objekt von (n-1)-dimensionalen Objekten begrenzt wird. Der Klassiker ist der 3-dimensionale Würfel der von sechs 2-dimensionalen Würfeln (Quadraten) begrenzt wird, wie fast jedem bekannt ist. Dieser Fall ist in der dritten Zeilen der Tabelle unten angegeben. Betrachtet man die Tabelle genauer, erkennt man rasch eine entsprechende Systematik und die daraus ableitbare Formel. Für die Würfel lautet sie n = 2d für die Dreiecke n = 1 + d (d: Anzahl Dimensionen, n: Anzahl Grenzfiguren).
| Dim | Würfel | Dreieck | ||
|---|---|---|---|---|
| 1 | 2 × 0D-Würfel | 2 Punkte begrenzen die Strecke | 2 × 0D-Dreiecke | 2 Punkte begrenzen die Strecke |
| 2 | 4 × 1D-Würfel | 4 Strecken begrenzen das Quadrat | 3 × 1D-Dreiecke | 3 Strecken begrenzen das Dreieck |
| 3 | 6 × 2D-Würfel | 6 Quadrate begrenzen den Würfel | 4 × 2D-Dreiecke | 4 Dreiecke begrenzen die Pyramide |
| 4 | 8 × 3D-Würfel | 8 Würfel begrenzen den Hyper-Würfel | 5 × 3D-Dreiecke | 5 Pyramiden begrenzen die Hyper-Pyramide |
Wir wissen nun, dass unser 4-dimensionaler Würfel aus der Aufgabenstellung von acht 3-dimensionalen Würfeln begrenzt wird. Aber wie sieht der Schatten genau aus?
Der 2D-Schatten des 3D-Würfels wird in den meisten Fällen wie links oben abgebildet dargestellt. So ist er für uns am besten zu erkennen. Würde man aber nicht schräg aus einiger Distanz auf den Würfel Blicken, sondern senkrecht auf ein Fläche und von ziemlich nah, käme das Bild unterhalb zustande. Bei dieser Variante ensteht in unserer Vorstellung nur selten ein Würfel und trotzdem ist es ein korrekter Schatten. Das Quadrat aussen rum (rot) ist das Quadrat, das dem Betrachter am nächsten ist. Das Quadrat innen (grün) ist das am weitesten weg. Die vier seitlichen Quadrate sind zu den vier Trapezen verzerrt worden (dreifarbig).
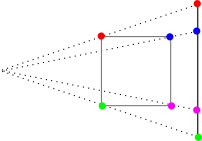
Das analoge Bild ergibt sich auch, wenn man einen Schatten eines 2-dimensionalen Würfels betrachtet. Am besten markiert man dabei die Ecken farblich, damit man erkennt was geschieht. Die Strecke, die dem Betrachter am nächsten liegt (rot-grün), wird gross abgebildet, die am entfernteste (blau-violett) am kürzesten. Die beiden anderen rutschen zur Seite.
Diese Systematik können wir nun auf den 3-dimensionalen Schatten des 4-dimensionalen Würfels extrapolieren. Aussen wird ein grosser Würfel sein. Der kommt von dem, der dem Betrachter am nächsten ist. Im Zentrum dessen ein zweiter kleinerer Würfel, der vom Entferntesten kommt. Die übrigen sechs Würfel sind zu Viereck-Pyramiden-Stümpfe verzerrt worden (das Pendant zum Trapez im 3D-2D-Fall). Das Ergebnis ist unten rechts abgebildet, links statisch, daneben als Animation. Ganz rechts ist ein einzelner der sechs verzerrten Würfelschatten abgebildet.
Wir können uns zwar immer noch nicht vorstellen, wie ein 4-dimensionaler Würfel aussieht. Seinen 3-dimensionalen Schatten hingegen können wir uns nicht nur vorstellen, wir können ihn sogar nachbauen und anfassen (wiederum am besten als Kantenmodell).
Prinzipiell könnte man mit dem gleichen Vorgehen 3-dimensionale Schatten von fünf und höher-dimensionalen Würfeln berechnen. Nur sind dazu mehrere Schattenwürfe nacheinander notwendig, was die Sache noch komlexer macht.
Wie sehen die Schatten von
n-dimensionalen Dreiecke aus?
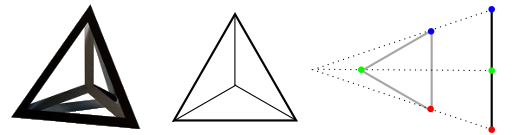
Ziemlich simpel: Aussen ein grosses n-dimensionales Dreieck, an dessen Aussenbegrenzungen vier, drei respektive zwei weitere n-dimensionale Dreiecke – leicht gestaucht – mit den Spitzen im Zentrum des Ersten.